Rainbow Equation 3F Rainbow Cube
The 3F Rainbow Cube (3f.r.cube) is at the very center of the Rainbow Equation. It is the central axis point from which the a./b./c. axes flow. The 3f.r.cube is geographically in the center of the Rainbow Equation because it is the only 3D model that can physically represent the six directions of space. The observer sees the manifest world about from the directions of left/right, front/back and top/bottom. This is why the cube is used to represent the center of the observer's perspective and the center of the Rainbow Equation. The 3f.r.cube is composed of 27 smaller hollow cubes. Each smaller cube is a total of 12 sectors: 6 inside and 6 outside.
The 3f.r.cube is considered third frequency because there is a third stacking of cubes in the three directions left/right, front/back and top/bottom with a total of 9 smaller cubes per wall of cubes in each direction. The total sectors on the shell inside (54) and shell outside (54) is 108 or 9 neutral polarity rainbows: (9sectors*6sides)=54 sh.o. The total of the inside sectors is162 or 18 neutral rainbows. This makes the grand total of sectors in the 3f.r.cube 324 or 27 neutral rainbows.
The rainbow equation for 3F Rainbow Cube is as follows:
sh.o.=(tri.s.*18=54)...+...i.s.=(quad.s.*18=108)...=(18s.=162)...+
sh.i.=(quad.p.*18=54)...+...i.s.i.=(tri.p.*18=108)...=(18p.=162)...
=(18s.+18p.)...=(324=27n.)
or expressed:
(sh.o.=18tri.s.)+(sh.i.=18quad.p.)=9n.
(i.s.=18quad.s.)+(i.s.i.=18tri.p.)=18n.
| The 3F Rainbow Cube aligns with the directionality of space left/right, front/back and top/bottom. |
Since the 3f.r.cube aligns with the directionality of space the rainbow polarities flow naturally left/right, front/back and top/bottom. On the shell of the 3f.r.cube is the tri-colors of orange-green-indigo. These colors determine the combination of inside in-between sectors depending on the axis they appear. In the orange axis the in-between sectors are a combination of walls of nine in red and yellow colors. The green combines blue-yellow and the indigo axis is blue-violet. If the inside in-between walls of the 3f.r.cube were translucent with the combination of any of these two blending colors then one could shine a light through them a produce the shell colors for the left/right, front/back and top/bottom axes. The 3f.r.cube is the only model of the Rainbow Equation that lines up directly with the directions of space this way. The natural blending of both the translucent and painted rainbows are operational in its structure.
| Both the translucent and painted rainbows are operational in 3F Rainbow Cube structure. |
As with all the hollows of the 3D models the inside are primary polarity rainbow colors and the outside sectors are secondary. To count the tri. and quad. secondary polarity rainbow combinations the patternization aligns: Quad. secondary=1red, 2yellow, 2blue, 1violet. Tri. secondary.= 1orange, 1green, 1indigo. The patternization for primary polarity rainbow is: Quad. primary=1/2red, 1yellow, 1blue, 1/2 violet. Tri. Primary=2orange, 2green, 2indigo. As shown in illustration 3.3 and table 8.2, colors flow using the secondary polarity rainbow colors on the outside of the 3f.r.cube and 27 smaller cubes, complemented by primary polarity colors facing the hollows. They alternate back and forth when moving any of the six directions – left/right, front/back and top/bottom along the walls of nine smaller squares. Illustration 8.6 shows the color flow for the 3f.r.cube. The colors on the outside of the “[ ]” are in the secondary colorization, while the colors inside the “[ ]” are are primary facing the hollows of smaller cubes.
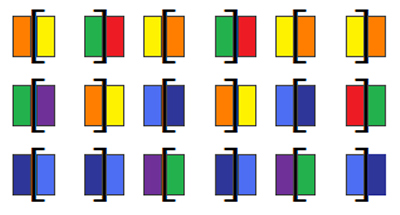 The 3f.r.cube is
1st. sh.o., i.s. <o,>r,<y,>r,<y,>o
The 3f.r.cube is
1st. sh.o., i.s. <o,>r,<y,>r,<y,>osh.i., i.s.i. >y,<g,>o,<g,>o,<y
2nd. sh.o., i.s. <g,>y,<b,>y,<b,>g
sh.i., i.s.i. >v,<o,>i,<o,>i,<r
3rd. sh.o., i.s. <i,>b,<v,>b,<v,>i
sh.i., i.s.i. >b,<i,>g,<i,>g,<b


